When and how to cluster standard errors in experimental data?

Recently, a colleague asked me how to cluster standard errors for a particular set of experimental data. This colleague conducted a multi-period experiment in which participants interacted in some form of group repeatedly over time. My initial response was to cluster standard errors on the participant level because unobserved components in outcomes for each participant across periods may be correlated to each other. Also, a layman's argument for participant level clustering is that it is the most “robust” form of clustering because you account for possible correlations at the lowest, most precise level possible. While participant level clustering is certainly plausible for this particular set of experimental data, this example led to a lot of questions about clustering standard errors in experimental data analyses. For instance, why shouldn't my colleague cluster at the group level? After doing some reading, I discovered that choosing when and how to cluster in experimental data is not only more complicated than I thought, but the discussion around it is quite recent.

A few working papers theorize about and simulate the clustering of standard errors in experimental data and give some good guidance (Abadie et al. 2017; Kim 2020; Robinson 2020). Next to more complicated, advanced insights into the consequences of different clustering techniques, a relatively simple, practical rule emerges for experimental data. Specifically, experimental researchers can ascertain whether and how to cluster based on how they assign treatments to participants. For experimental reseachers, clustering is, therefore, an experimental design feature that can be determined before conducting the experiment. Specifically, clustering is appropriate when it helps address experimental design issues where clusters of participants, rather than participants themselves, are assigned to a treatment. I have summarized the practical guidance for clustering in experimental data in the diagram below.

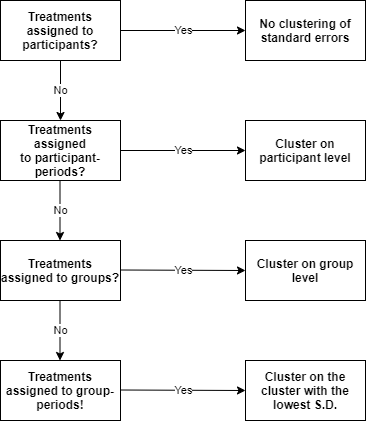
I will walk through the diagram from top to bottom. Please consider the following empirical specification: $$y = a + b.Treatment + e$$ If $Treatment$ is assigned at the participant level and you conducted a one-shot experiment, then there is no need to cluster standard errors. Abadie et al. (2017) is a useful reference explaining why this is not necessary, but the reasoning is relatively simple. Since $Treatment$ is assigned to participants, unobserved components in outcomes for each participant is randomized across treatments.

As soon as $Treatment$ is assigned on a cluster rather than the participant level, then the clustering of standard errors may be appropriate. Various possible design features may warrant clustering, but the two most common features are that (1) $Treatment$ is assigned to participant-periods (in multi-period experiments) and (2) $Treatment$ is assigned to groups of participants (e.g., teams, markets, and experimental sessions). In case $Treatment$ is assigned to participant-periods, participant level clustering can be inherited from the experimental design. When $Treatment$ is assigned to groups of participants, then group level clustering is appropriate.

But what would the advice for my colleague, who assigned $Treatment$ to group-period sets of data, be? In this case, both participant and group level clusters can be inherited from the experimental design. Thus, my colleague must choose a cluster! A useful rule of thumb put forward by Kim (2020) is to check standard deviations of the observations within each potential cluster. Recall that the residuals of the simple empirical specification above are the deviations from a conditional mean. A sufficiently smaller within-cluster standard deviation compared to the standard deviation of the whole observations may imply that the residuals flock together, and hence they are correlated within the cluster.

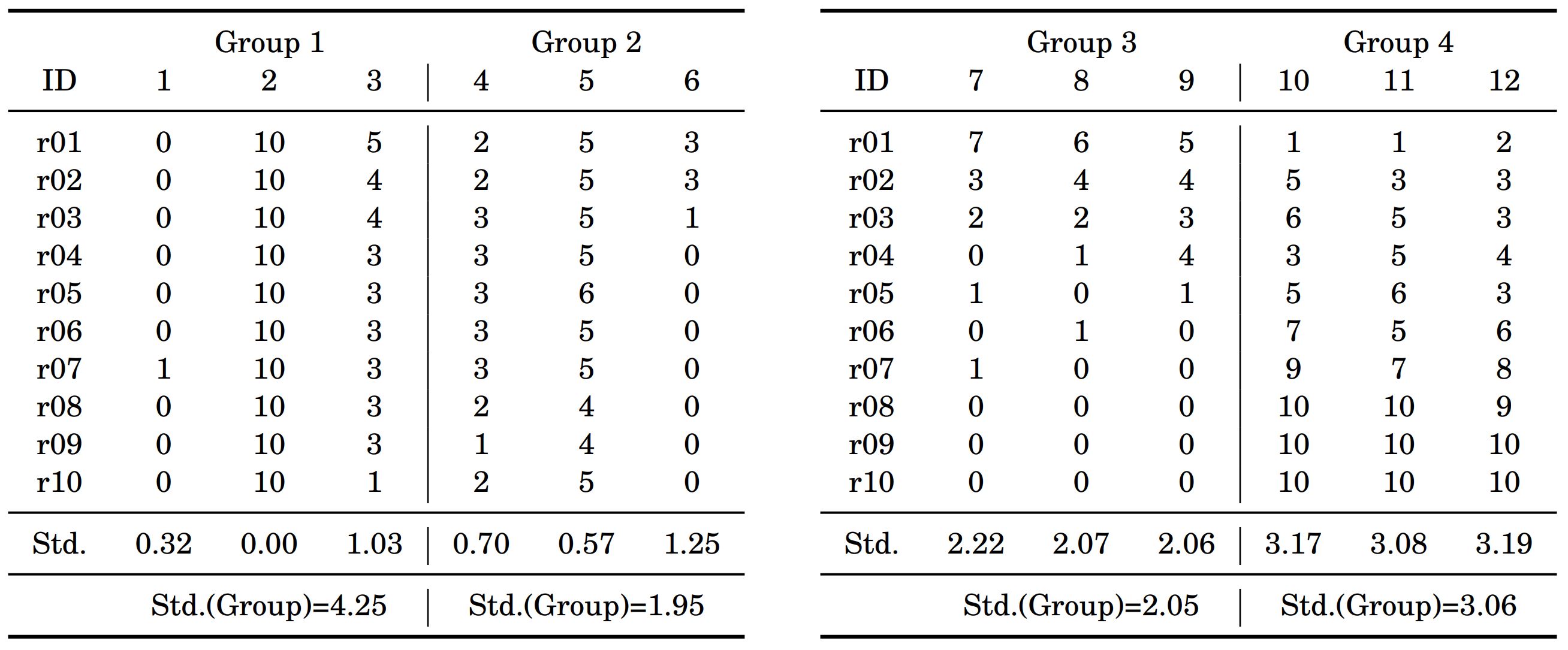
Please consider the hypothetical data, provided by Kim (2020), above. The example features experimental data in which $Treatment$ has been assigned to fixed groups of participants who repeatedly interact over 10 periods. The potential clusters are the participant level and the group level. The standard deviations of participant-period sets of observations are smaller than group-period sets of observations. Thus, in this case, you may want to cluster at the participant level. However, if standard deviations of group-period sets of observations would be smaller than the participant-period sets of observations, then you may want to cluster at the group level.

But what do you do if you have assigned $Treatment$ to participants who interact in groups over time but reform their groups randomly and anonymously at the start of every period? This experimental design falls into the category “Treatments assigned to participant-periods” because the group cluster is randomized every period. The only remaining observational similarity in the experimental data is caused by asking each participant to make repetitive decisions in the same environment. Thus, clustering at the participant level is inherited from the experimental design.

Summary

Recently, practical advice emerged for clustering standard errors in experimental data analyses. This advice bases the decision of when and how to cluster mainly on the features of the experimental design. There may be other potential clusters that experimental researchers could consider besides the ones central to the examples above. For instance, the central premise of Kim (2020) is the consideration of session level clustering, which could be relevant if treatments are assigned to experimental sessions. I did not consider this example because experimenters typically take great care in either assigning different treatments within experimental sessions or making sure that the conditions under which experimental sessions are held are as consistent as possible.

References

Abadie, A., Athey, S., Imbens, G. W., & Wooldridge, J. (2017). When Should You Adjust Standard Errors for Clustering? Available at: https://arxiv.org/pdf/1710.02926.pdf.
Kim, D. (2020). Clustering Standard Errors at the “Session” Level. Available at: https://ssrn.com/abstract=3635181.
Robinson, T. (2020). When Should We Cluster Experimental Standard Errors? Available at: https://tinyurl.com/y4yj9uuj

How to reference this online article?

Van Pelt, V. F. J. (2020, July 18). When and how to cluster standard errors in experimental data? Accounting Experiments, Retrieved from: https://www.accountingexperiments.com/post/clustering/.