'Effect sizes don't matter in experiments.' Or do they?

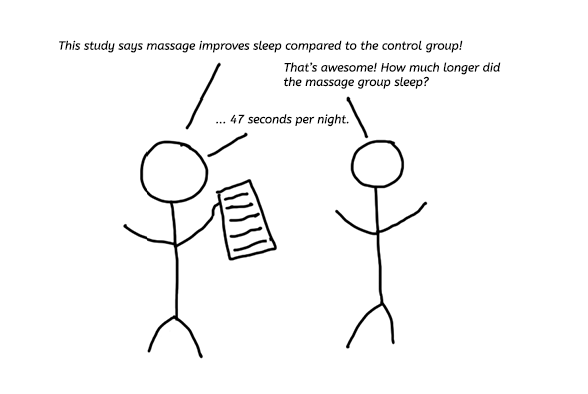
During accounting conferences, seminars, and workshops, I have repeatedly heard the statement: ‘effect sizes do not matter in experimental accounting research.’ It is often a response to inquiries from the audience about how well the interventions under experimental examination perform. This statement is typically followed by the argument that experimental accounting research only aims to test directional hypotheses (positive versus negative and larger versus smaller) because they are easier to generalize to naturally-occurring settings and practice. In accounting, we prefer experimental research that has the potential to offer policy implications for organizations, firms, and institutions in practice.

In this post, I explain why it is essential, from a statistical point of view, to report effect sizes and why they do matter if we want to offer potential policy implications to practice. In what follows, you will uncover that not reporting effect sizes, and solely relying on statistical significance, promotes rather undesirable practices among experimental accounting researchers. You will also learn that refusing to talk about effect sizes is equivalent to putting on blinders when testing your directional hypotheses. Specifically, it is taking the position that your experimental intervention can be potentially effective while refusing to have a more thorough discussion about what its potential effectiveness could be.

What is effect size precisely?

Effect size $=\frac{\bar{x}_t - \bar{x}_c }{\sigma}$

Effect sizes quantify the (relative) size of the difference between two groups and may, therefore, be said to be a true measure of the significance of differences. Although there are many ways to calculate effect sizes, a straightforward method is Cohen's d. It takes the mean difference between the group with the intervention and the control group and divides it by the population's standard deviation. Unfortunately, the standard deviation of the population is often unavailable. As a result, we typically use the standard deviation from the control group or a pooled set of values from both the group with the intervention and the control group. Cohen's d is similar to a Z-score, making it relatively easy to convert it into useful statements. For instance, an effect size of 0.6 means that the average person's score in the experimental group is 0.6 standard deviations above the average person in the control group.

Relying on statistical significance alone promotes undesirable research practices

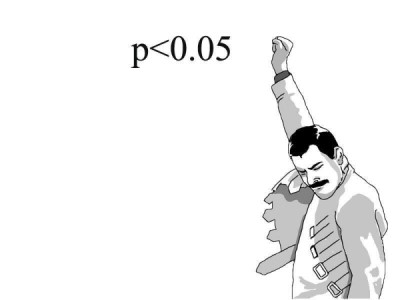Although effect sizes appear relatively unpopular in experimental accounting, statistical significance is not. However, there are several problems with relying on statistical significance alone to test hypotheses. It is usually calculated as a p-value, which is the probability that a difference of at least the same size would have arisen by chance, even if there is no actual difference. As soon as we estimate a p-value lower than some arbitrary threshold (e.g., p < 0.05), we conclude that we have found a significant effect of the intervention under experimental examination.

The p-value depends essentially on two things: The size of the effect and the sample size. One way to generate a ‘significant’ result is to focus your study on huge or rather obvious effects (even if you only have a relatively small sample). Another way to get a significant result is to acquire a massive sample (even if the effect you are considering in your study is tiny or rather meaningless). Thus, solely relying on statistical significance promotes undesirable practices like (1) gathering massive samples via platforms, such as M-turk and Prolific and (2) prioritizing our focus on interventions with huge or rather obvious effects.

Since it is commonly-accepted to report only one statistical measure (i.e., statistical significance), experimental researchers fixate on this specific measure while losing sight of others. When combined with incentives, such as publication and tenure, experimental researchers may be inclined to ‘search’ for statistically significant results during the analyses. They may exploit their discretion to conduct and report analyses until nonsignificant results become significant or even directly misreport p-values, a process generally referred to as p-hacking. Recent research shows evidence that p-hacking also happens in experimental accounting (Chang et al., 2021). The benefits and opportunity to engage in p-hacking are far lower if we decide that experimental researchers should also report other statistical measures like effect size measures.

Although this portrays a rather bleak picture for statistical significance, it is not a meaningless metric. Statistical significance helps boost our confidence that an observed difference is not merely coincidental. Accordingly, it is still a useful metric together with other metrics, such as the size of the sample, power, degrees of freedom, and the size of the effect. However, statistical significance does not tell us the most critical thing: It does not tell us anything about how well the intervention under experimental examination performs relative to some benchmark or comparison in the same or a very similar experiment.

Experimental accounting research tests the potential effectiveness of interventions

One of the weaknesses of experiments is that they score low on mundane realism, reflecting the degree to which the materials and procedures involved are similar to events that occur in the real world. However, experiments also have strengths. One of their selling points is that they are well-suited to identify the causal effects of interventions, such as policies and systems (i.e., their potential effectiveness), with meticulous precision. Therefore, a key purpose of experiments is calibrating design elements carefully to generate differences between experimental groups. Therefore, the design decisions we make as part of the intervention are the entire reason why we conduct the experiment in the first place! Proposing that the observed size of the effect is a meaningless metric is similar to proposing that experiments are of little value to accounting.

Experiments are of value to accounting, and effect sizes can increase their value in a more scientific way. Effect sizes help shift the discussion from whether an intervention can potentially be effective to how effective it could potentially be and why. By emphasizing the most crucial aspect of an experimental intervention, i.e., the size of the effect, rather than exclusively its statistical significance (which conflates effect size and sample size), we can use experiments to examine interventions’ potential effectiveness better. When we find experimental support for a rather weak effect, future experiments could change the intervention or add a second intervention to increase the effect and vice versa. This process would also help us uncover why and when the intervention could potentially be effective if we hadn't thought about it before. However, it could also be that some interventions are just not that effective in experiments while others are very effective. What do you think a practitioner prefers to learn about? Do you think he or she prefers to learn that an intervention can be potentially effective or that he/she also would like to learn what its potential effectiveness could be and why?

Complementing experimental analyses with effect size measures also helps promote a more uniform body of experimental accounting research. Unlike statistical significance, experimental accounting researchers can use effect size measures to compare and combine the results of multiple similar experiments and conduct meta-analyses. Consequently, they allow experimental accounting researchers to build more strongly on each other's work and establish a more coherent view about what experimental evidence shows about the effectiveness of certain interventions and what is driving it.

Conclusion

As accounting researchers, we know all too well that no metric is perfect. Thus, we may not want to keep betting all our money on the same horse (i.e., statistical significance). But why are effect sizes so unpopular in accounting relative to other social science fields that conduct experiments? One possible explanation is that effect size calculations are also less extensively covered in standard statistics and econometric courses. Another explanation could be that experimental researchers confuse discussions about effect sizes with discussions about (1) differences in means versus (2) actual means. Specifically, the means of experimental groups are rarely insightful in isolation because they are driven by the specific design features that are shared between groups. Instead, it is the difference in means that is typically the focus of experimental research. It turns out that that is precisely what effect size calculations aim to capture. I hope that incorporating effect size calculations into our results sections becomes a standard for future experimental accounting research.

References

Chang, X., Gao, H., & Li, W. (2021). P-Hacking in experimental accounting studies. Available at: https://ssrn.com/abstract=3762342.

How to reference this online article?

Van Pelt, V. F. J. (2020, September 17). ‘Effect sizes don't matter in experiments’ Or do they? Accounting Experiments, Available at: https://www.accountingexperiments.com/post/effect-size/