Why you shouldn't trust mediation as process evidence
TL/DR
- Mediation involves testing the effect of an independent variable on a dependent variable through a mediating variable. Its low cost and easy integration have made it the standard form of process evidence for experimental studies, including those in accounting.
- However, the inclusion of a mediating variable messes up random assignment and biases the relationship between the mediating variable and the dependent variable, no matter at what point the mediating variable is measured during the experiment.
- As a result, mediation tends to overestimate the indirect path while underestimating the direct path, leading to invalid conclusions about causal mechanisms.
- There are alternative experimental techniques, such as moderation-by-process designs and conducting multiple experiments, that outshine mediation in obtaining valid and reliable process evidence. This is primarily because they leverage the USP of experiments: Randomization and causal inference
What is process evidence?
If you are familiar with experimental research, particularly in the field of accounting, then you probably have heard of the term “process evidence.” It is data that helps establish the underlying causal mechanisms through which manipulated independent variables affect measured dependent variables. Process evidence is a highly sought-after (if not a necessary ingredient) of a finished experimental paper. While there are different ways to obtain process evidence in experiments, mediation is the most popular form by far because it is cheap and easy to include in experimental designs. However, there is a hefty, and typically overlooked, price tag, which invalidates it as a strong form of process evidence. In this post, I explain why mediation is the worst type of process evidence for experimental research. I also discuss two other well-known techniques that offer much stronger process evidence.
Mediation at a glance
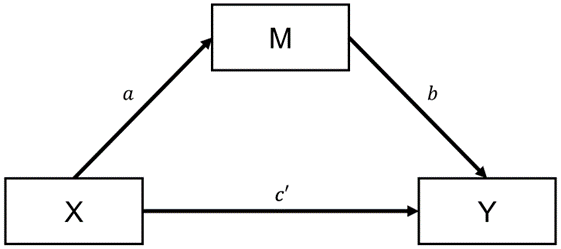
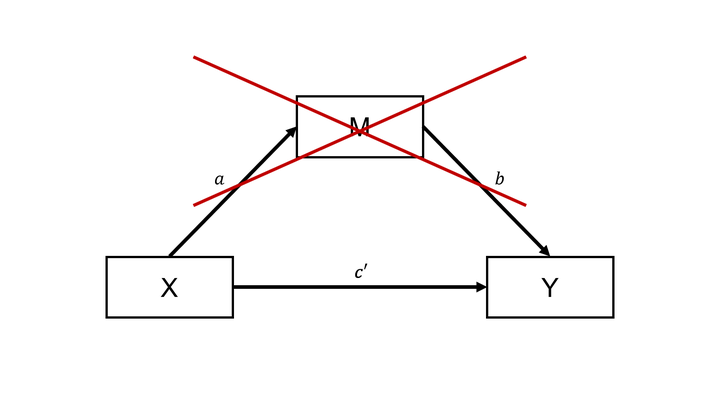
Figure 1: Mediating relationship $b$etween $X$ and $Y$.
Mediation involves testing whether a manipulated independent variable $X$ affects a measured dependent variable $Y$ “through” a measured mediating variable $M$ (see Figure 1). There is evidence for mediation when $X$ influences $M$ (relationship $a$), which, in turn, influences $Y$ (relationship $b$). Unlike $X$, $M$ is endogenous and not manipulated by the experimenter. Instead, $M$ is either unobtrusively measured during the experiment or elicited interim or ex post. These two approaches to measuring mediating variables each have their merits and problems (Asay et al., 2022), but that is not the focus of this post. We did write a post about the often overlooked limitations of ex post techniques, such as post-experimental questionnaires, in this post I wrote with Farah Arshad.
The mediation trap
Besides being low-cost and immensely popular in fields like accounting, there is a trap when using mediation as process evidence. When we statistically find support for an indirect effect ($a$ × $b$), one may be quick to reason that it provides strong support for the causal mechanism ($X$ → $M$ → $Y$). Given that the independent variable $X$ is randomly assigned, one might expect there is no correlated omitted variable bias. That is kind of why we run experiments in the first place. That expectation does apply to the empirical model without mediation, i.e., one that only tests for the causal effect of $X$ on $Y$. Specifically, that simpler empirical model typically leads to an unbiased estimation of the causal effect $c$ (see Figure 2).
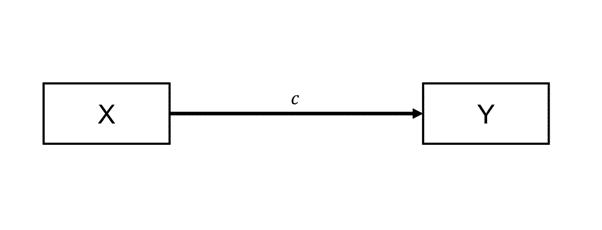
Figure 2: Causal relationship $b$etween $X$ and $Y$.
However, this reasoning does not apply to the empirical model that also estimates the mediating path going from $X$ to $Y$ through $M$ (see Figure 1). Including $M$ in the empirical model messes up random assignment, which makes relationship $b$ (between $M$ and $Y$) and $c’$ (between $X$ and $Y$) generally biased. Relationship $b$ between $M$ and $Y$ is biased because, while it picks up the causal effect (if any) of $X$, it also picks up the confounded effect of all things that correlate with $M$ outside the experiment. It does not matter when and how $M$ is measured. As soon as it is measured, there is a reasonable possibility that $M$ is subject to classic omitted variable bias. This particular bias in $M$ is perhaps not new to some because Asay et al. (2022) also highlight it as a weakness of using mediation as a process evidence. However, what is generally overlooked is that the bias in $M$ spreads to $X$, leading to bias in the mediating effect ($a$ × $b$).
The bias also spreads to relationship $c'$ (the direct path between $X$ and $Y$). Since we test mediation by subtracting $c’$ from $c$, we underestimate (overestimate) $c’$ if the sign of the bias in $b$ is positive (negative). Thus, the sign of the bias in $c’$ is the sign of the correlation between $M$ and $Y$ outside the experiment. In most cases, the model in Figure 1 will overestimate mediation and underestimate $c’$. In extreme cases, the positive bias in $b$ can even lead us to infer there is an indirect “causal” effect via $M$, while in reality there is no effect of $X$ on $Y$ (Rohrer, 2019). It is theoretically possible (but improbable) to underestimate mediation while having a positive bias in $c’$. For instance, if, for some strange reason, the correlation between $X$ and $M$ is positive in the experiment, but the correlation between $M$ and $X$ is negative outside of it.
So what is the intuition?
This dangerous problem with mediation has been covered in the statistical literature and popular outlets outside of accounting (see, for instance, MacKinnon and Pirlott (2015), Rohrer et al. (2021), and Data Colada (2022)). The intuition behind the problem can be illustrated using a simple example (see Figure 3). Let’s say you are interested in how an intervention $X$ affects employees’ performance Y, and your causal mechanism states that the intervention $X$ will lead employees to be more productive ($M$), which, in turn, leads to higher performance $Y$. Thanks to randomization, $M$ includes some productivity free of confounds caused by the intervention $X$. However, it also includes productivity related to confounds, like employees being passionate about their job, enjoying the type of tasks they are doing, or caring about being a high-performer.
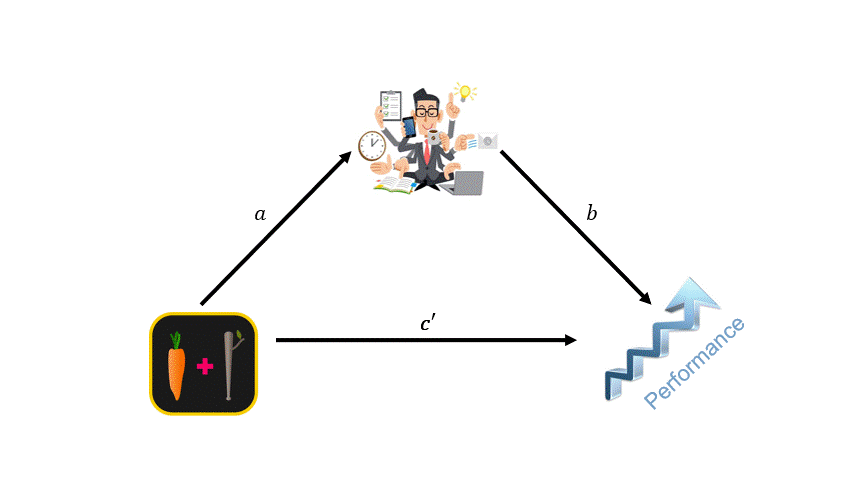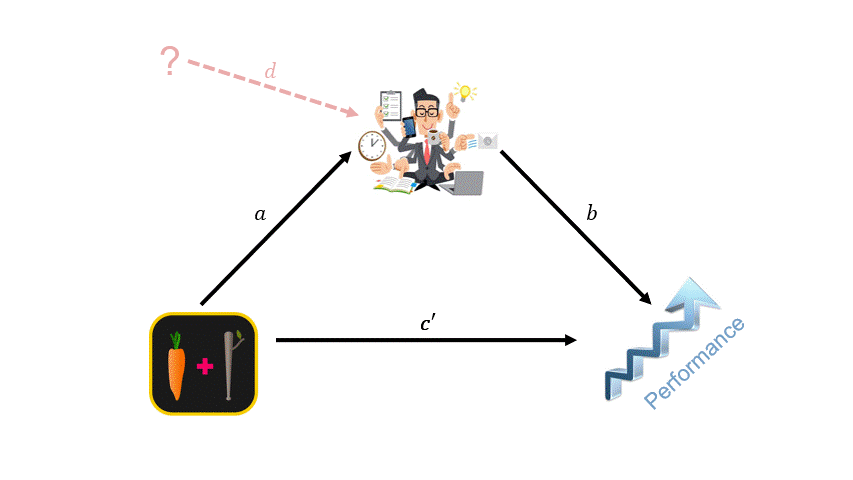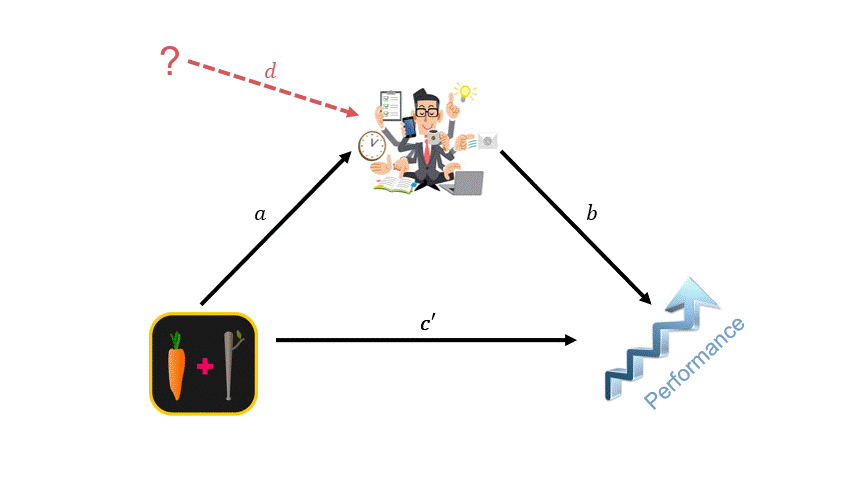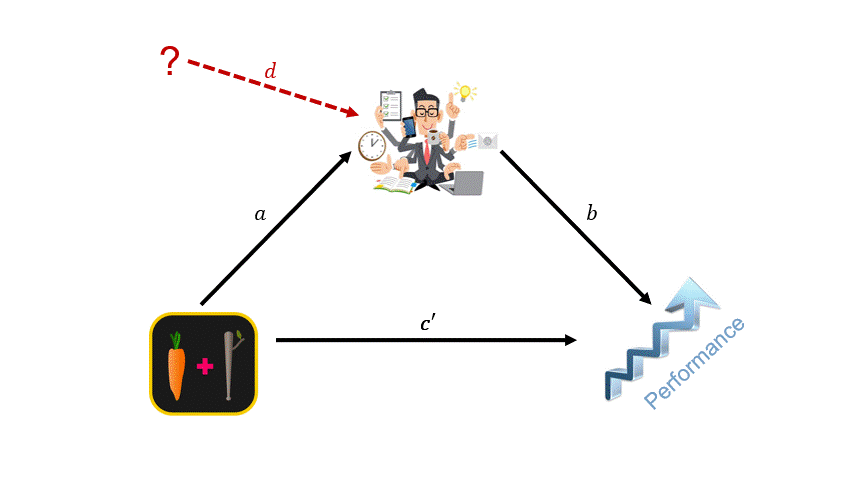
Figure 3: Illustrative example.
This simple example illustrates that the relationship $b$ will be a combination of the causal and confounded effects of productivity, which, in turn, will bias the mediation effect and the direct effect. The size of the bias will depend on the relative impact of the counfounding factors. If the causal effect of a 1% increase in productivity equals a 4% performance increase and the confounded effect is an 8% increase in performance, then we would estimate the increase in performance to be higher than the causal effect (i.e., 8% > $b$ < 4%). Thus, we would overpredict the increase in performance due to the intervention via the productivity path. Also, the model in Figure 3 would bias $c’$ downwards by the average error arising from $b$ being inflated toward 8%. Unlike this example, we do not precisely know how large the confounded effect will be, making it difficult to infer how close we are to the true indirect effect and whether this will show up as statistically different from zero in our analyses.
So what? Isn’t everything biased?
Nothing is perfect. Even the magic of randomization can fail. However, the primary point is that mediation is generally biased in an otherwise relatively clean experiment. Experiments’ comparative advantage is identifying causal effects. I.e., their strength is using randomization and implementing interventions to observe how it produces variation in a dependent variable of interest. Its comparative advantage is not making surveyesque path models that infect otherwise relatively clean causal effects. It is a bit like showing up at a funeral in your party outfit. The party outfit may be very impressive, but it is just not befitting a funeral. Thus, as far as a weakness goes for a particular process evidence technique, mediation seems particularly undesirable for experiments. The problem cannot be resolved by unobtrustively measuring mediating variables. Nor does it make sense to start including lots of control variables in some post-experimental questionnaire. Namely, you would basically be changing your methodology from an experiment to a survey.
Alright, but are there alternatives?
There are other ways to obtain process evidence that outshine mediation (Bullock and Green, 2021). These techniques build much more strongly on the experiment’s ability to establish causality. The only weakness these alternative techniques have are weaknesses of the experimental method itself. The first technique is moderation-by-process designs. It involves manipulating a second independent variable in addition to a first. The purpose of the second independent variable is to change the causal mechanism central to the first in a conceptually consistent way. If the data show that the second independent variable indeed modifies the causal relationship generated by the first, we have obtained process evidence of the first.
A second technique is to conduct multiple experiments sequentially and have each build on the others. One approach would be to conduct an initial experiment establishing the causal effect of $X$ on Y, followed by two more that test for the causal effects of $X$ on $M$ and $M$ on $Y$. This would be the “experimental” way to lay bare some conceptual path if you want to but it does not make great use of the experiments’ primary strengths. An approach that leverages these strengths better is zooming in or out of the causal mechanism. An initial experiment could identify a rather broad relationship $b$etween $X$ and $Y$. This broad relationship $c$ould focus on a bigger picture, while capturing multiple theoretical processes. Followup experiments could try to eliminate some of the theoretical processes at play. For instance, a followup could change one aspect of the experimental design or the independent variable $X$ to narrow the causal mechanism.
Conclusion
If we use mediation to obtain process evidence for an experiment, we expect $X$ to lead to $M$ and $M$ to lead to $Y$. If we expect that indirect path, we should also expect confounding variables to explain the correlation between $M$ and $Y$ outside the experiment. This type of correlation invalidates mediation because it tends to overestimate the indirect path while underestimating the direct path. This could lead to wrongly inferring that there is evidence for an indirect path while a correlated omitted variable bias drives it. There are ways to obtain process evidence that leverage the strengths of the experimental method much more, like including moderating variables that change the causal process and conducting multiple experiments to zoom in or out of the causal process.
References
How to reference this online article?
Van Pelt, V. F. J. (2023, April 11). Why you shouldn't trust mediation as process evidence. Accounting Experiments, Available at: https://www.accountingexperiments.com/post/mediation-is-biased/.